I wrote my first post covering the Fibonacci Sequence two years ago in April 2014. The original post was written with Objective-C sample code and only considered one possible solution. A few months later, to my surprise, Apple had a session at WWDC called Advanced Swift which covered some of the approaches used below. I thought this would be a great time to provide an update to the original post but with a bit more detail.

The Fibonacci sequence is a special sequence of numbers. The first two numbers are 0 and 1. The numbers in the sequence after that build on these first two numbers. The pattern is the next number in the sequence is the sum of the two previous numbers.

The Fibonacci sequence begins like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc…

A few years ago I was interviewing at multiple companies. One interviewer asked me how I would generate a Fibonacci number at a given index.

For example: Given 0: return 0; Given 1: return 1; Given 2: return 1; … Given 20: return 6765.

I started by writing a method that would solve the problem through brute force using recursion, but it wasn’t really what the interviewer was looking for. I fumbled through the question and didn’t get an offer from that company.

Recursion

Let’s take a look at what I was trying to do during this interview.

The code would look something like this in Swift:

Recursive Fibonacci

Look at how many times that method is called for a relatively small index (20). 21,891 times! That’s not really a good way to do it.

I then took it one step further. I had it calculate the first 29 Fibonacci numbers. This process resulted in the recursive method being called 2,692,507 times, which took about 8 minutes (in Xcode Playgrounds). That’s just not scalable. Let’s try another approach.

Memoization

During the interview, I had thought that we could cache some of the results. This would allow us to access Fibonacci numbers that had been generated much faster. I wasn’t aware at the time that this technique is called memoization.

This technique will help optimize the calls once a result has been generated. Since this is a recursive approach which depends on previous calculations, this approach is much more efficient. Let’s look.

I tweaked the code in our recursion example to include memoization. You can see that the code isn’t that much more complex. The caching was easy enough to add. The bonus here is that if we call fibanocciaAtIndex for a given index more than once, the answer is immediately returned.

Memoized Fibonacci First Run

This time when I calculated the same relatively small index (20), the call count is much smaller, only 21 times.

Memoized Fibonacci Second Run

I then had it calculate the first 29 Fibonacci numbers. The results were calculated much faster and with fewer calls. This is a huge improvement over the pure recursive appraoch.

Golden Ratio — Binet’s Fibonacci Number Formula

Is there another approach? One where you don’t need recursion? Of course there is. I didn’t figure out this approach until well after that interview, which prompted the original blog post.

I did more research into the Fibonacci Sequence and discovered that you can calculate these numbers using the Golden ratio.

The Golden ratio is defined mathematically as:

Golden Ratio

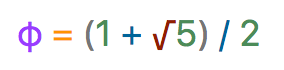
Or φ ≅ 1.618034…

It turns out you can use the Golden ratio to calculate numbers in the Fibonacci sequence. This is Binet’s Fibonacci number formula:

Binet’s Fibonacci Number Formula

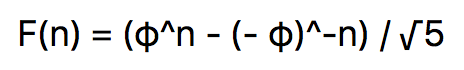
This is a much cleaner approach to the original recursive approach above. Instead of dealing with recursion, which can be tricky, this is a straightforward method to calculating Fibonacci numbers.

Here’s what that looks like in code:

Binet's Fibonacci Number Formula Code

Large Numbers

In my original post, I had some thoughts about how to handle larger numbers. Unfortunately, I never made any progress there. I think once I posted the original blog post, I lost interest in dealing with really large numbers. There are a few interesting projects like OSXGMP and BigInteger that may work here. I’m including them for reference, in case you’re interested in larger numbers.

Conclusion

There are probably other ways to figure out a Fibonacci number at a given index. I’ve gone through three methods above. I wouldn’t recommend the first approach. Recursion with memoization is probably the cleanest of the approaches and doesn’t require a lot of math.

Just for fun, I’ve put these code samples up of GitHub. The project includes both Swift examples (in Xcode Playgrounds) and Objective-C examples (written using CodeRunner 2). Feel free to get them and play with them.

GitHub Repo: rwgrier/fibonacci-sequence

Thanks to Keith Elliott

Swift 2.0 included a number of new language statements. I recently wrote about the Swift Guard Statement. Defer is another statement new to Swift 2.0. Honestly, I don’t use defer as much as guard, but it can be extremely useful.

What defer does is not obvious at first. Defer will wait to execute a block of code until the current scope (loop, method, etc) is exiting. And it will execute that code whether the scope is exiting cleanly, from a guard, or while an error is being thrown.

Here’s the most basic of examples. The defer block exists before the main body of the code, but it’s not called until afterwards.

func simpleDefer() {
	defer {
		print("Leaving.")
	}
		
	print("Main body of the function.")
}

This can be useful if, for example, there are resources you need to ensure are cleaned up before leaving the current scope.

You don’t need to limit yourself to a single defer statement. You can use multiple defer statements. When more than one are included, they will be called in reverse order. Think of them being included on a stack and popping them off one at a time.

Here’s a simple example of multiple defer blocks. You can see that the order they are defined and the order they are called is reversed.

func multipleDefer() {
	defer {
		print("one")
	}
	
	defer {
		print("two")
	}
}

As I’ve stated above, the defer statement isn’t just limited to exiting from methods. You can include them in loops. Look at this example. Everytime the loop is executed, the defer block is called at the end of each loop.

func simpleLoopDefer() {
	var multiplier: Int = 1
	for i in 0..<5 {
		defer {
			print("loop count: \(i); multiplier: \(multiplier)")
		}
		
		multiplier += multiplier * i
	}
}

If you’re coming from the world of Objective-C or Java, you can approximate the defer statement with a finally block from a throw statement. The syntax is a little different and in Objective-C and Java, you aren’t allowed to have multiple finally blocks. Here’s a Swift example of a defer block being used like a finally block.

func throwsDefer() {
	defer {
		print("clean up from error and non-error states")
	}
	
	do {
		try methodThatCanThrowError()
	}
	catch {
		print("Why??? What did I do??")
	}
}

There is a caveat to using the defer statement. In a defer code block, you cannot transfer control outside of the current scope. You can’t call “return” out of a function, or “continue” out of a loop.

I believe that defer is one of the lesser used statements in Swift. I don’t think it will be used as often as guard. I could probably utilize defer more than I currently am. But it can be useful, so check it out.

GitHub Repo: rwgrier/swift-defer

Swift 2.0 added the guard statement to the language. Guard is not new with Swift, it’s been around for a while in other programming languages, such as Haskell and Erlang.

Guard statements are very simple and effective. They ensure the check you are performing is true before continuing on. If the result of that check is false the else statement executes, which usually exits a function.

Here’s a very simple example:

func submitForm() {
	guard (validationResults == .valid) else {
		return
	}
	
	// Build form request and submit.
}

All this does is check the hasValidData variable to see if it’s true. If not, the function exists. This can easily be done with an if statement, like this:

func submitForm() {
	if (validationResults != .valid) {
		return
	}
	
	// Build form request and submit.
}

Here’s a less simple example. I can’t say more complex, because it’s slightly contrived just to give a taste of how this could go. The guard statement does a few things here. It checks the optional (UITextField.text property) for a value, unwraps it and assigns it locally. If that check fails, the validation fails and the method exits gracefully.

func validateFormGuard() {
	guard let username = usernameField.text, let password = passwordField.text else {
		return
	}
	
	guard username.lengthOfBytes(using: String.Encoding.utf8) > 3 else {
		validationResults = .invalidUsername
		return
	}
	
	guard password.lengthOfBytes(using: String.Encoding.utf8) > 3 else {
		validationResults = .invalidPassword
		return
	}
	
	guard usernameExists(username) else {
		validationResults = .usernameExists
		return
	}
	
	validationResults = .valid
}

This could also be done with if statements:

func validateFormIfs() {
	if let username = usernameField.text, let password = passwordField.text {
		if username.lengthOfBytes(using: String.Encoding.utf8) > 3 {
			if password.lengthOfBytes(using: String.Encoding.utf8) > 3 {
				if !usernameExists(username) {
					validationResults = .valid
				}
				else {
					validationResults = .usernameExists
				}
			}
			else {
				validationResults = .invalidPassword
			}
		}
		else {
			validationResults = .invalidUsername
		}
	}
}

If you are checking a lot of properties and conditionals, the if statements can become more nested and can get into a Pyramid of Doom scenario. The guard statement cleans this up and gives you more readable code.

Guard statements aren’t just for easy function exits. You can use them in loops, where if you don’t meet the conditional, proceed onto the next item in the loop (using continue instead of return).

Guard is an extremely useful mechanism in Swift. It allows you to clean up your code. If you’re writing code in Swift, check them out.

GitHub Repo: rwgrier/swift-guard

The Fibonacci sequence is a special sequence of numbers. The first two numbers are 0 and 1. The numbers in the sequence after that build on these first two numbers. The pattern is the next number in the sequence is the sum of the two previous numbers.

The Fibonacci sequence begins like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc…

Last summer I was interviewing at multiple companies. One interviewer asked me how I would generate a Fibonacci number at a given index.

For example:

Given 0; return 0.
Given 1; return 1.
Given 2; return 1.
...
Given 6; return 8.

I started by writing a method that would solve the problem through brute force using recursion, but it wasn’t really what the interviewer was looking for. I fumbled through the question and didn’t get an offer from that company.

Once the interview was over, I made a few half-hearted attempts to figure this out (which I had on Github), but wasn’t happy with anything. I forgot about this entirely until a few weeks ago, when I decided to figure it out.

I did more research into the Fibonacci Sequence and discovered that you can calculate these numbers using the Golden ratio.

The Golden ratio is defined mathematically as:

    (1 + √5)
φ = -------
       2

Or φ ≅ 1.618034…

It turns out you can use the Golden ratio to calculate numbers in the Fibonacci sequence. This is Binet’s Fibonacci number formula:

         φ^n - (- φ)^-n
F(n) = ----------------
               √5

This is a much cleaner approach to the brute force approach for calculating these numbers. Instead of dealing with recursion, which is tricky, this is a straightforward method to calculating Fibonacci numbers.

Here’s what that looks like in code:

Obj-c code

#define SQRT_5 sqrt(5)
#define PHI ((1 + SQRT_5) / 2)

...

+ (unsigned long long) fibonacciAtIndex: (NSUInteger) index {

    if (index < 2) {
        // Save some cycles.
        return index;
    }

    // x(n) = (Phi^n - (-Phi)^-n) / √5
    long double numerator = powl(PHI, index) - powl((long double) (-1.0 * PHI), -1.0 * index);
    long double fibonacci = numerator / SQRT_5;

    return (unsigned long long) fibonacci;
}

Larger numbers?

This method above is accurate until an index of 71, after that the numbers drift enough to be noticeable. I haven’t spent much time figuring out how to handle larger numbers. I could probably try NSDecimalNumber or BIGNUM.

I don’t know if this is the best way to generate Fibonacci numbers for a given index. If/When I look into handling larger numbers may find this to be a terrible approach.